

A LASER ( Light Amplification by Stimulated Emission of Radiation) is an electromagnetic oscillator which combines light amplification with feedback. The laser uses mirrors to feed the light output from an optical amplifier through a delay (the travel time of the light) back into the amplifier input.
A laser is capable of producing an intense beam of photons having identical scalar and vector properties (frequency, phase, direction and polarization). As a result, a laser beam can be bright, monochromatic, coherent, and unidirectional.
Quantum mechanics predicts that all atomic and molecular systems are characterized by discreet energy levels. These energy levels are the eigenvalues of the Hamiltonian of the system and the corresponding states are its eigenstates. The state corresponding to the lowest possible energy level is termed the ground state and the states corresponding to the other levels are termed excited states. If the energy of the system is measured at any time, the result of the measurement will be one of the energy eigenvalues, and after the measurement the system will be in the corresponding eigenstate.
In a dense medium, such as a solid, liquid, or high pressure gas, frequent collisions between the atoms or molecules cause transitions between energy levels. Optically allowed transitions can also change the energy of the system. An optically allowed transition between energy levels involves the absorption or emission of a photon with frequency f, such that hf = ∆Eif, where ∆Eif is the energy difference between the initial and final energy level and h is Planck’s constant. If the angular momentum quantum number li of the initial state and the angular momentum quantum number lf of the final state differ by 1, i.e. if ∆l = ±1, then a transition involving a photon is very likely. If ∆l ≠ ±1, then a transition involving a photon is much less likely. If no lower lying state satisfying ∆l = ±1 exists, an excited state is called meta-stable. ∆l = ±1 is called a selection rule. If this selection rule is not satisfied, an optical transition is forbidden (unlikely).
An atom or molecule can emit a photon via spontaneous emission or stimulated emission. Atoms and molecules in excited states randomly emit single photons in all directions according to statistical rules via spontaneous emission. In the process of stimulated emission, a photon of energy hf perturbs an excited atom or molecule and causes it to relax to a lower level, emitting a photon of the same frequency, phase, and polarization as the perturbing photon. Stimulated emission is the basis for photon amplification and it is the fundamental mechanism underlying all laser action.
Consider the simple case of a two-level system with lower level 1 and upper level 2. The rate of absorption and stimulated emission depends on the number of photons present. Quantum mechanics lets us calculate those rates. The probability that the system in level 1 absorbs a photon is equal to the probability that the system in level 2 emits a photon via stimulated emission. The rate of spontaneous emission, however, is independent of the number of photons present. Stimulated emission becomes much more likely than spontaneous emission if many photons are present.
The competition between absorption, stimulated emission, and spontaneous emission defines the criteria for laser action.
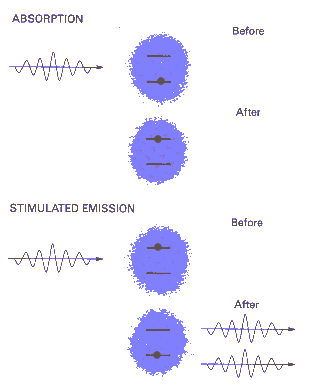
Consider the simple case of a two-level system with lower level 1 and upper level 2. Let N1 be the number density of atoms in level 1 and N2 be the number density in level 2.
In thermal equilibrium N1 > N2. As a resonant photon is more likely to be absorbed than to stimulate emission. But if N2 > N1 there is the possibility of average overall amplification for an array of photons passing through a volume of atoms of the two-level system. This situation is termed population inversion, since under normal conditions N1 > N2.
Spontaneous emission depletes N2, producing unwanted photons with random phases, propagation directions, and polarizations. Because of loss associated with spontaneous emission and other losses associated with the laser cavity, each laser is characterized by a minimum value of N2 - N1, termed the threshold inversion. Only if N2 - N1 is greater then the threshold inversion do we see laser action.
There are several ways of pumping a system to produce a population inversion. It is, however, impossible to optically pump a two-level system, since once N2 = N1 the induced transition rate equals the absorption rate. Three or four levels are needed to pump the system and produce the population inversion required for laser action. Let us investigate the pumping of a four-level system.
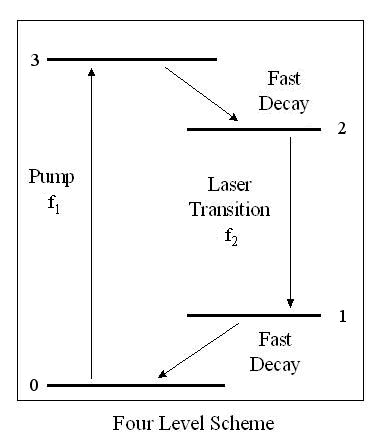
An atom is first excited by optical, electrical, or other means through the “pump transition” from a starting level “0” to a temporary level or group of levels “3”. The atom quickly relaxes to a metastable level “2”. Stimulated emission occurs from level “2” to level “1”. Level “1” quickly decays back to level “0”, so that absorption from level “1” to level ”2” is unlikely. At any given time more of the atoms are at level “2” than at level “1”, there is a “population inversion”. The rate of stimulated emission will exceed the absorption rate resulting in an optical amplifier.
Solid systems are usually pumped by optical means with intense light. Xenon-filled flashtubes are positioned alongside the lasing medium. A high voltage electric discharge is passed through the flashtubes, causing them to emit an intense flash of white light. This light is partially absorbed by the amplifying medium. A flashlight-pumped laser has a pulsed output.
Gaseous systems are often pumped by passing an electric discharge through the medium itself. Lasers that are pumped by an electric discharge can produce either a pulsed output or a continuous output depending upon whether the discharge is pulsed or continuous.
Laser diodes are pumped by passing an electric current through the diode junction. They can produce either a pulsed output or a continuous output.
To sustain laser action it is usually necessary to place the lasing material between the two mirrors of an optical cavity. Some possible cavity designs are shown below.
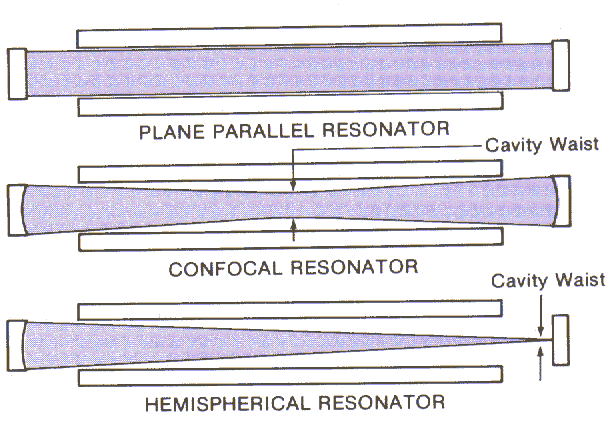
Photons are reflected back and forth through the lasing medium, which greatly increases the probability of stimulated emission. Because a coherent beam makes multiple passes through the optical cavity, we observe an interference-induced longitudinal mode structure. Only light whose wavelength satisfies the standing wave condition, mλ = 2L, will be amplified. L is the cavity length and m is a large integer referring to the number of nodes in the standing wave pattern. Out of phase reflections are lost through destructive interference. Spontaneously emitted photons with off-axis velocity components escape from the lasing volume and are not significantly amplified.
The resonant frequencies of a cavity of length L are fm = c/λ = mc/(2L). The separation between resonance frequencies is ∆f = c/2L. A typical visible wavelength laser resonator might have length L = 30 cm operating at wavelength λ = 600 nm so that m = 1 million. For an L = 30 cm resonator, the spacing between successive resonance frequencies is ∆f = c/2L = 500 MHz while the resonance frequencies are near fm = c/λ = 500 THz, one million times larger. Non-relativistic quantum mechanics predicts that atomic and molecular systems have stable excited states with discrete, well defined energy eigenvalues. But we observe that all excited state spontaneously decay. The uncertainty principle, ∆E∆t ~ ħ, then requires that the energies of the excited states, and therefore transition frequencies, cannot be known with arbitrary accuracy. We have ∆f∆t ~ 1/(2π). Several of the resonance frequencies fm may fall into that range ∆f. The spectrum emitted by a laser is a combination of the resonant frequencies fm that fall into that range ∆f. A representative laser output spectrum is shown below.
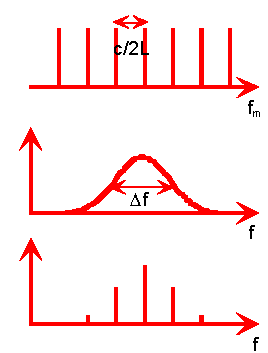
Modified laser resonators can suppress all but one of the resonant frequencies, permitting more precise control of the frequency, a desirable feature in scientific and engineering applications
The gain per pass varies greatly between different types of lasers and so do mirror requirements. Pulsed lasers tend to exhibit higher gain per pass than continuous wave (CW) lasers, although the massive population inversion can only be maintained for a small interval of time. A typical helium-neon laser has a single pass gain of the order of 1% and requires high reflectance mirrors (100% and 99%). Lasers that are capable of producing multiple wavelengths from several different lasing transitions require specially optimized mirrors if output at each wavelength is desired.
In-class activity: Laser activity
The radiation field may have nodes and antinodes in the plane perpendicular to the laser axis. The different transverse irradiance patterns are referred to as Transverse Electric and Magnetic (TEM) modes. In an unconfined cavity with cylindrical symmetry, these modes form simple progressions of irradiance functions. Transverse modes are identified by their irradiance distributions and are designated TEMpq where the subscripts p and q refer to the number of nodes along the two orthogonal axes perpendicular to the laser axis. The irradiance distributions of all the modes are smoothly varying but none has a uniform irradiance distribution.

The lowest order mode, TEM00 has a cylindrical Gaussian irradiance distribution.
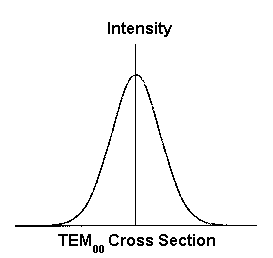
This mode experiences the minimum possible diffraction loss, has minimum divergence, and can be focused to the smallest possible spot. For these reasons, it is often imperative that the laser be restricted to operation in this mode. Higher order modes have a larger spread and suffer higher diffraction losses.
The Helium- Neon (He-Ne) Laser
For many years the most common CW
laser was the He-Ne laser. These low-power (mW) lasers use an
In a helium neon laser, a low pressure mixture of helium and neon (<15%) is contained in a narrow bore glass tube. A longitudinal, DC electrical discharge is maintained in the narrow tube. This creates a plasma. Collisions with free electrons in the plasma excite the helium atoms and cause a significant number of them to be trapped in the lowest energy metastable states. These are the 21S and the 23S states, where one of the two helium electrons has been raised from the lowest energy 1S atomic orbital to the 2S orbital. For this reason, they are termed electronically excited states. Neon is a larger, more complex atom, with 10 electrons which are arranged in a 1s22s22p6 configuration in the 1S0 ground state. Neon has many excited states, and the ones concerned with laser action are shown in the energy level diagram below. The multiplet nature of the electronically excited states arises from the number of different ways in which the angular momenta of the electrons can be combined.
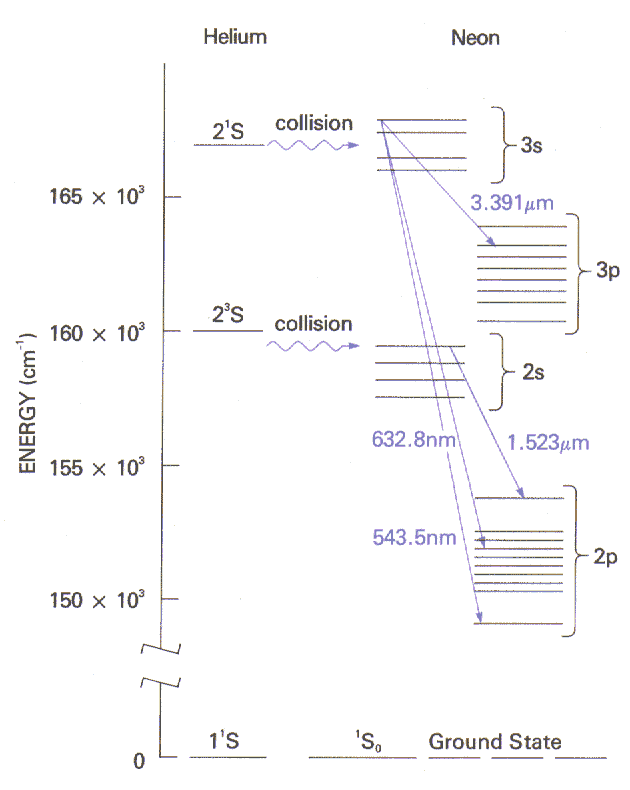
Two sets of excited states of neon (2s and 3s) occur at excitation energies similar to those of the 23S and 21S states of helium, which are favorably populated by the laser discharge. Within the plasma, atoms are rapidly colliding with other atoms, electrons, and with the walls of the tube. Collisions between excited state helium atoms and ground state neon atoms cause some of the neon atoms to be excited to the 2s and 3s states. (The labeling of these states is different from usual labeling of configurations and is explained here.) Collisional energy transfer is a resonant process in which the total energy is conserved. The small energy mismatch is compensated by changes in the kinetic energy of the atoms.
Most of the neon laser wavelengths utilize transitions into the 2p series of levels. For example, the 632.8nm red output is produced by the 3s2 - 2p4 transition. The 2p energy levels lie ~18.6 eV above the ground state and therefore are negligibly populated, even in the plasma. Consequently, a population inversion between 3s and 2p, and between 2s and 2p, in the ensemble of neon atoms in the plasma discharge is easily maintained by collisional pumping with excited helium atoms. Both the 3s - 2p and 2s - 2p transitions are optically allowed and hence can give rise to laser action. The 2p states are populated by the laser transitions but are rapidly depopulated by spontaneous emission to lower levels.
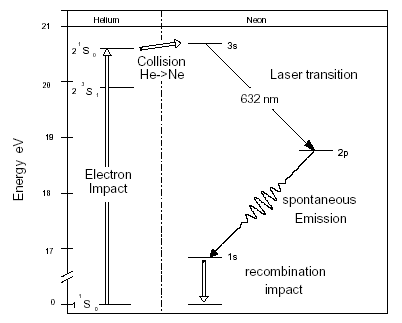
With the exception of the 3.391 micron line, helium neon lasers are all low gain devices and require cavity mirrors of high reflectance in order to achieve lasing action. Typically, one end of the cavity is defined by a total reflector (reflectance >99.9%), and the other end is defined by a mirror which permits ~ 1% of the intra cavity light to escape, forming the useful output of the laser. It therefore follows that the intra cavity beam is up to 200 times more intense than the output beam.
Links: